基本信息
- 论文: ATOM: A Grammar for Unit Visualizations
- 作者: Deokgun Park, Steven M. Drucker, Roland Fernandez, and Niklas Elmqvist
- 来源: TVCG 2018
背景
单元可视化(unit visualization)是一种区别于聚合可视化的形式。往往聚合可视化焦聚于生成具有统计结果意义的可视化形式,比如柱状图,饼图,直方图(histogram)等等;而单元可视化则使得每一个数据点都能够在可视空间中被绘制出来,比如散点图(scatterplot,下图 a),点图(dotplots,下图 b),单元图表(unit chart,下图 c)。
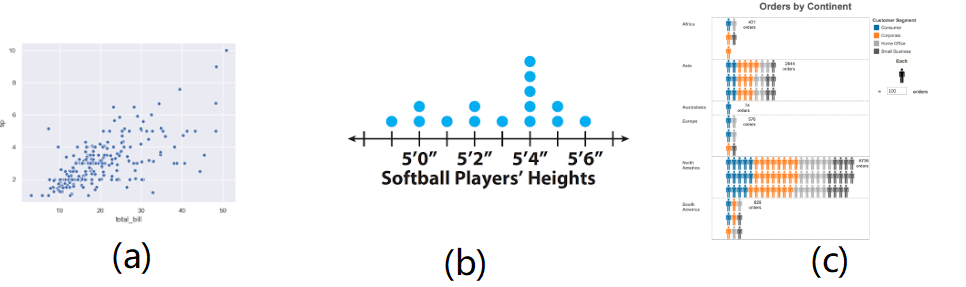
相较之下,聚合可视化能够解决视觉混乱的问题(visual clutter),而单元可视化因为其进行数据空间到可视空间一对一映射,其 computational scalability(内存、计算、渲染等)、display scalability(展示空间不足)和 perceptual scalability(人的处理能力)都会较差;但单元可视化也并未没有优势,它因为完全展示了所有数据点,故而能够进行异常值检测,并且能够提供在动画、交互过程中对个体元素进行追踪,并且这种一对一映射的单元可视化,更接近人们的思考和构建可视化时的思考习惯和认知,且还能解决一些更细致的交互需求。
基于上述特点,作者提供了一种高层次的单元可视化语法,它基于一次对设计空间的结构化探索,提供了自顶向下递归式的数据和空间剖分。
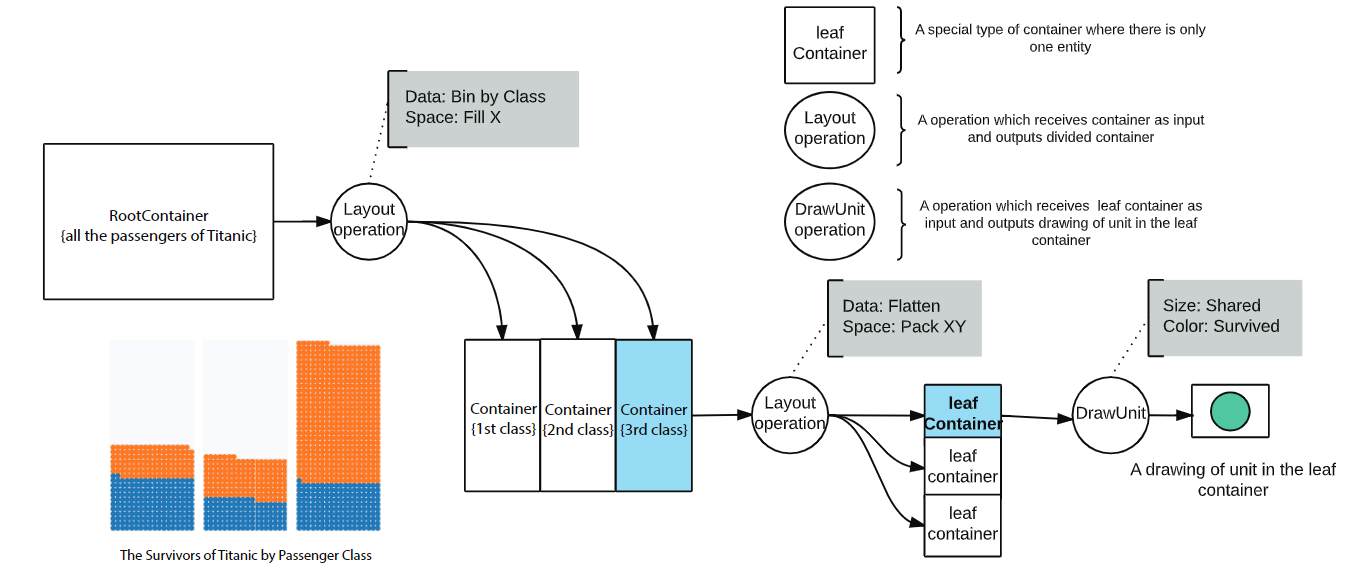
相关工作
作者对以往的单元可视化进行了一个分类,一直追溯到上古时期。对于他们的布局方法、坐标系统和单元图标进行了一些分类。
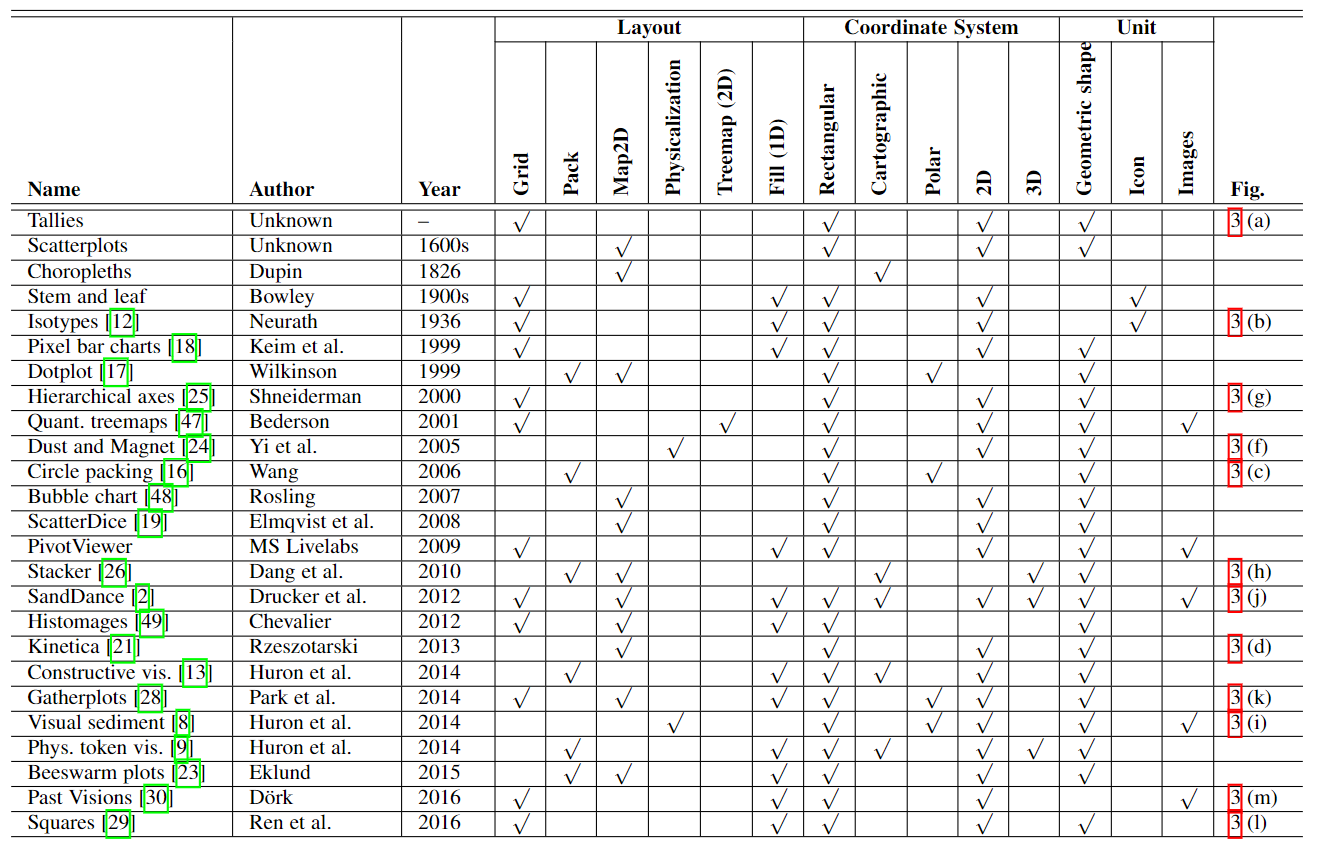

除此以外,作者还讨论了一些以往的可视化创作(语法)工具,比如 Prefuse/Processing/D3/Protovis 等编程式工具,ggplot2/vega/reactive-vega/vega-lite 等声明式工具等。
Design Space
在本文中,作者焦聚于静态的可视化形式,而不讨论任何交互、动画等。
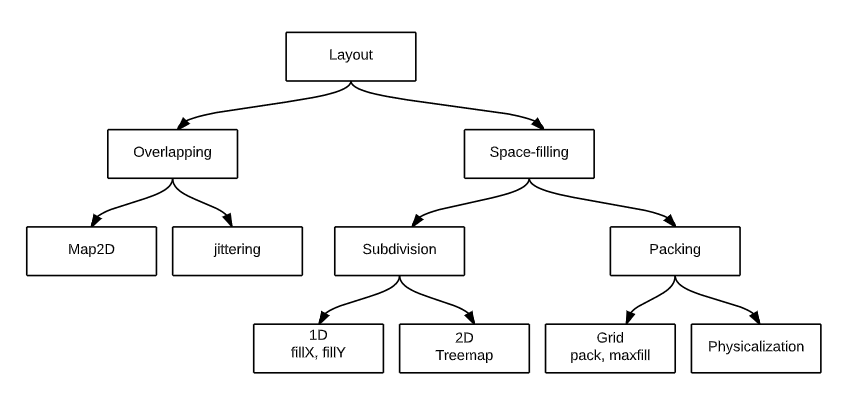
作者将布局类型划分成两类:重叠的和非重叠的。重叠的布局,每个数据点位置和大小只依赖于自身,比如散点图。非重叠的布局,其数据点位置和大小往往需要通过整体或者周围的数据点来决定,其一般是空间填充类型的,上图的大部分可视化都是如此。对于这种类型,又可以分成两种手段,一种是划分(subdividing),即自顶向下分配可视化空间;另一种是填充(packing),则是自下向上把空间挤满(这种可视化形式,每个数据点往往是正方形或正圆形,横纵比 1:1)。
对于每个点的表达,又可以大致分成两种:一种是静态的预定义好的几何形状(比如一个 icon 或者 image),一种是根据数据自身决定的(比如不同类别绘制不同形状,glyph 等等)。
ATOM
接下去,作者开始讨论语法的设计。ATOM 主要要解决以下几个问题:
数据空间的操纵,作者定义了四种方法:
- BIN:可以对数据进行分类 or 聚类;
- FILTER:根据某种过滤类型过滤数据;
- DUPLICATE:数据拷贝
- FLATTEN:数据平面化,不再进行任何聚类,直接将数据一对一绘制;
可视空间的划分:在这里,作者将以往存在的划分手段进行了一个层次划分,但最后只实现了以下几种:
- Map2D:直接用数据中的特征将数据映射到可视空间中(最常见的就是 scatterplot)
- FillX&FillY:对一维空间进行填充
- MaxFill:对整个空间寻找一个最大填充的解(类似背包问题)
- Pack:类似上面的 MaxFill,但是每个图形都是方正的
上述的几种手段,具体效果可以见下图;上面一行表示的是均匀划分,下面一行则是加权平均进行划分;
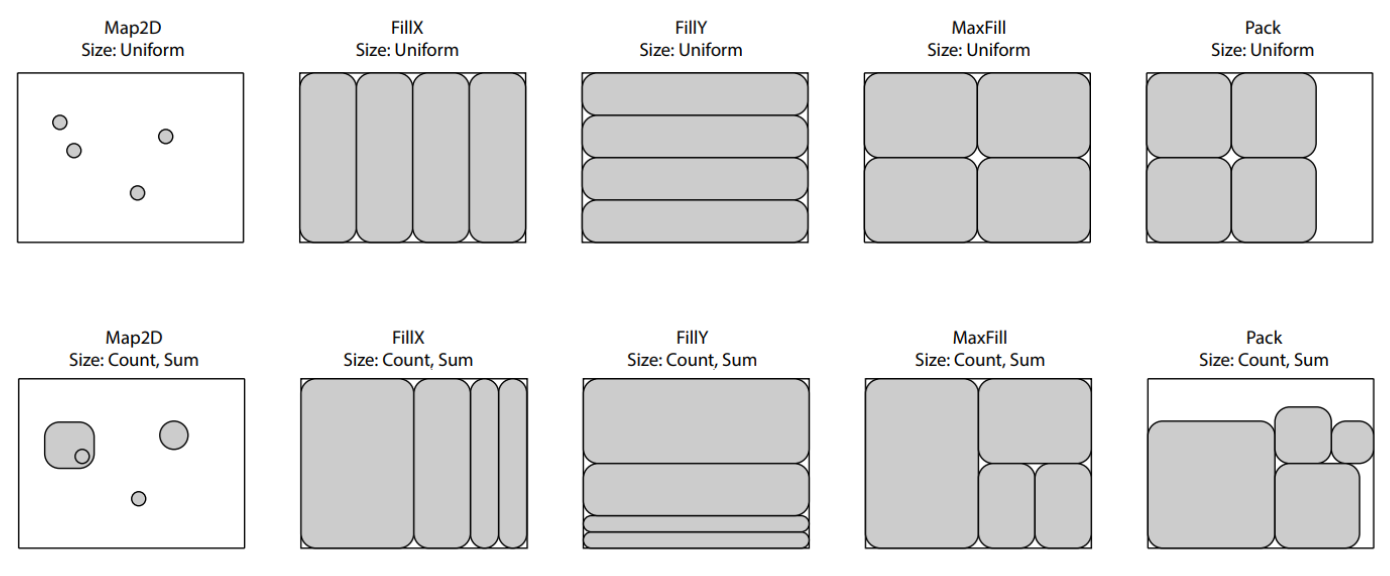
单位外观的问题
shape 是长方形还是圆形?
大小是 uniform 的还是根据 count/sum 进行的;
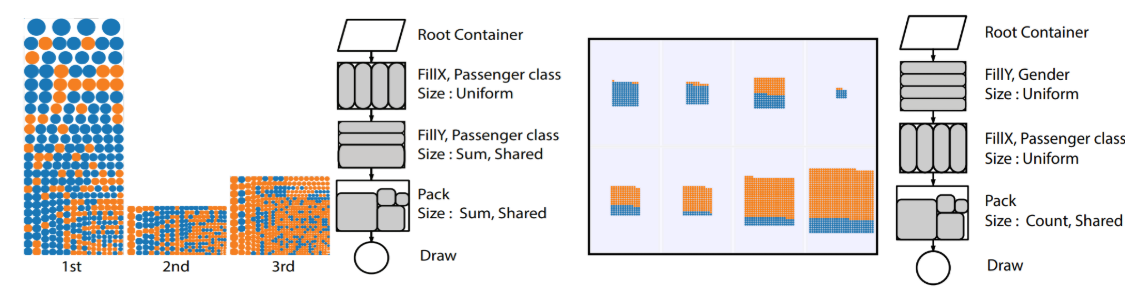
isShared 属性;也就是,单位大小是否要根据隔壁组进行统一?该配置项大概效果如下图,左边是三列共享大小,右图则是不共享。
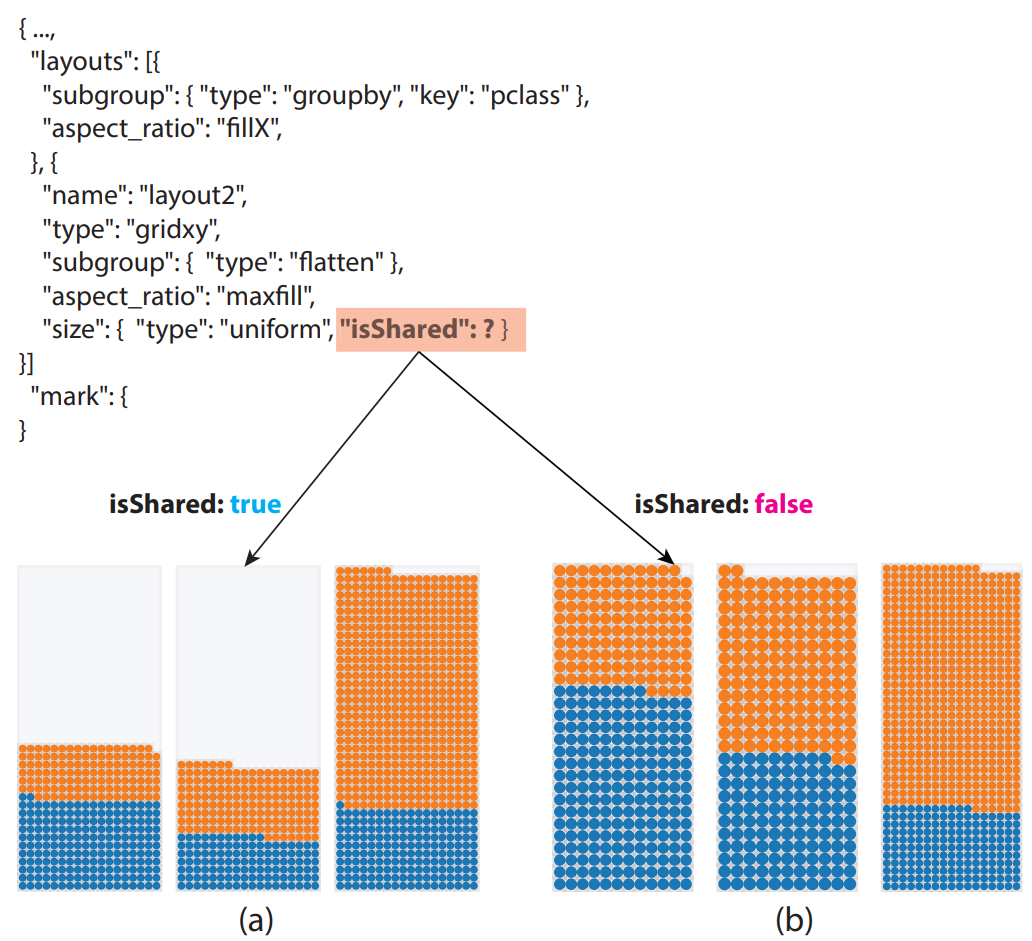
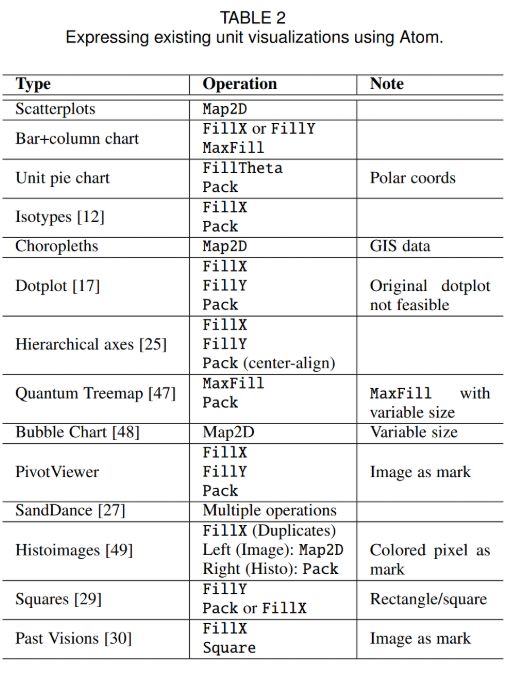
评估
最后,作者进行了两次评估。为了证明其表达力,作者罗列了为了解决以往存在的不同单元可视化形式,用 ATOM 可以怎么进行详见下面的表格;为了证明其生成可视化的能力,作者又创作了两种不曾存在的可视化形式。